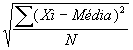Com esta base de dados criada será mais fácil compreender as provas estatísticas.

1.1 Interpretar as frequências absolutas e relativas.

No caso de variáveis nominais como o sexo ou a raça, só poderão ser calculadas as frequências. É totalmente impossível calcular a média ou a mediana do sexo porque a escala destas variáveis não tem sequer uma relação de ordem. Repare-se que por vezes codificam-se as variáveis com números para introdução no computador, o que torna possível pedir erradamente médias para variáveis nominais, embora tais resultados, evidentemente, não tenham significado nenhum!

No caso de variáveis ordinais ou quantitativas, claro que é também possível calcular as frequências. Por exemplo, suponhamos que sabemos o Peso medido em Kg de 1000 pessoas. Será possível calcular as frequências de quem tem 40 Kg, 41 Kg, 42 Kg, ..., etc., mas atendendo ao elevado número de pessoas, será preferível agrupá-las em grupos com o mesmo intervalo, por exemplo, grupo A (40-45 Kg), grupo B (46-49 Kg), etc., de forma a calcular as frequências para cada grupo.

Convém que o intervalo de amplitude dos diferentes grupos seja sempre o mesmo, caso contrário, os resultados poderão confundir-nos, pois tenderemos a comparar grupos que não são comparáveis! [1]

1.2 Interpretar as médias, desvios-padrão, medianas, etc.

Para além das frequências absolutas e relativas já referidas, existem outras medidas geralmente calculadas para variáveis ordinais ou quantitativas, tal como se encontra no quadro seguinte:

A Média aritmética assim como o Desvio-padrão que lhe está associado, são conceitos que geralmente oferecem poucas dúvidas. São calculados apenas em variáveis com a escala quantitativa. Por exemplo, não tem significado calcular a média para o Sexo (variável nominal) ou para o Peso medido em escala ordinal.

O conceito de Mediana, no entanto, gera muitas confusões: a Mediana é simplesmente o valor que se situa a meio da fila ordenada de valores, desde o mais baixo ao mais alto. Assim, tem que haver uma relação de ordem nos valores, pelo que a Mediana pode ser calculada tanto para as variáveis ordinais como para as quantitativas puras. A partir do exemplo relacionado com a base de dados "Experiência" criada no EpiInfo, poderemos criar uma nova variável idade a partir da data de nascimento e data actual, tal como se explica no Manual sobre o EpiInfo, e executar o comando MEANS para a idade, obtendo todas estas medidas. Neste exemplo, temos cinco pessoas com as seguintes idades já ordenadas:

O número 27 representa o valor que está a meio, ou seja, é a Mediana. Isto significa que 50% das pessoas têm uma idade igual ou maior que 27 e, evidentemente, os outros 50% têm uma idade igual ou menor que 27.

O número 20 representa o valor que está a meio da primeira metade, ou seja, é o primeiro Quartil ou Percentil 25. Isto significa que 75% das pessoas têm uma idade igual ou maior que 20 e, evidentemente, os outros 25% têm uma idade igual ou menor que 20.

O número 39 representa o valor que está a meio da segunda metade, ou seja, é o terceiro Quartil ou Percentil 75. Isto significa que 75% das pessoas têm uma idade igual ou menor que 39 e, evidentemente, os outros 25% têm uma idade igual ou maior que 39.

Claro que a mediana é também o segundo Quartil e o Percentil 50. No caso deste exemplo, com um número ímpar de valores ordenados (cinco), a mediana é o valor que está a meio, mas no caso de um número par de valores ordenados, a mediana terá ser calculado fazendo-se a média entre os dois valores que estão a meio.

A Moda é o valor mais frequente (ou seja, o que "está na moda"...). Neste caso, como não existe nenhum valor mais frequente, o EpiInfo dá-nos o menor valor (através do comando MEANS), o que não tem significado absolutamente nenhum, podendo mesmo induzir-nos em erro. O que se passa é que quando existem várias Modas, o EpiInfo apresenta sempre a menor: ou seja, se numa amostra existem 10 pessoas com 20 anos e 10 pessoas com 30 anos, sendo todas as outras idades menos frequentes, sucede que existem duas Modas, mas o EpiInfo vai referir apenas a que apresenta o menor valor ou seja, dirá que 20 anos é o valor mais frequente. Por isto, se nos interessa referir a Moda, convém verificar se não há outro valor tão frequente na nossa amostra. Para isto basta executar o comando FREQUENCIES, que nos dá as frequências de todos os valores.

Qual a diferença de interpretação entre a Mediana e a Média?

Em primeiro lugar a Mediana pode ser utilizada tanto em variáveis quantitativas como em variáveis qualitativas ordinais, enquanto a Média só pode ser utilizada em variáveis quantitativas.

Em segundo lugar, no caso das variáveis quantitativas, embora a Média seja um valor mais fácil de entender, tem o defeito de nos induzir em erro se a nossa amostra tiver valores muito extremos. Por exemplo, na distribuição de idades da nossa amostra a Média é de 30,2 e a Mediana de 27. Imagine que o indivíduo mais velho tinha não 50 anos de idade mas sim 100 anos. Isto faria com que a Média saltasse para 40,2, ou seja, seria superior a quase todos os valores individuais, mas a Mediana continuaria a ser 27. Se olharmos para todos os 5 valores individuais da nossa amostra, verificamos que o número 27 é melhor representante da distribuição global da idade na nossa amostra que o erróneo número 40,2.

Assim, no caso das variáveis quantitativas, quando o valor da Mediana é muito diferente da Média, é aconselhável considerar sempre a Mediana como valor de referência mais importante.

Além das medidas de localização central (média, mediana, moda) existem as medidas de dispersão que nos dão a ideia da variação dos dados.

Quando se calcula a média dever-se-á sempre calcular o desvio-padrão, apresentando-se a sua fórmula apenas para ficar-se com uma ideia do que representa:

Ou seja, para calcular o Desvio-padrão é necessário primeiro calcular a Média e depois calcular todas as diferenças entre cada valor individual e a média. É um erro dizer que o desvio-padrão é a média de todas as diferenças, mas podemos senti-lo como algo aproximado.

Por vezes, queremos comparar duas variáveis quantitativas quanto ao seu grau de dispersão, por exemplo, o Peso (em Kg) e a Idade (em Anos). Esta comparação não poderá ser feita comparando simplesmente os Desvios-padrão respectivos, porque estes estão expressos em unidades de medida diferentes, i.e., não se pode comparar a dispersão de Kg com a de Anos! No entanto, é possível fazer esta comparação em termos relativos, se calcularmos o coeficiente de variação, da seguinte forma:

Nas variáveis ordinais, como não é possível calcular médias ou desvios-padrão, para avaliar o grau de dispersão, poder-se-á calcular a Amplitude interquartil e o Desvio-quartil.

A Amplitude interquartil é simplesmente a diferença entre o 3º e o 1º Quartil, ou seja, no exemplo anterior, 39-20= 19. Repare-se que nesta Amplitude inter-quartil situam-se os 50% centrais dos valores.

O Desvio interquartil é sempre metade da Amplitude interquartil, ou seja, 19/2=9,5.

Também é possível, calcular a o coeficiente de variação quartil da seguinte forma:

Claro que estes cálculos também podem ser efectuados para as variáveis quantitativas.